In questo articolo parliamo di sezione aurea facendo riferimento alla spiegazione di Franco Fontana nel libro Fotografia Creativa.
Dopo aver letto di tutto e di più su questo argomento, sono giunta alla conclusione che l’unico che è stato in grado di spiegarmela con pochissime parole, e in maniera estremamente efficace, è stato proprio il grande Fontana. Si tratta di una spiegazione che non si perde in cifre e calcoli complessi. Del resto, si sa che la comunicazione semplice è difficile da trovare. Trovi l’estratto alla fine dell’articolo.
SCOMPONIAMO UNA SEZIONE AUREA PER CAPIRE COME È FATTA:
Dato un segmento suddiviso in due parti, la parte maggiore deve stare alla minore come l’intera sta alla maggiore.
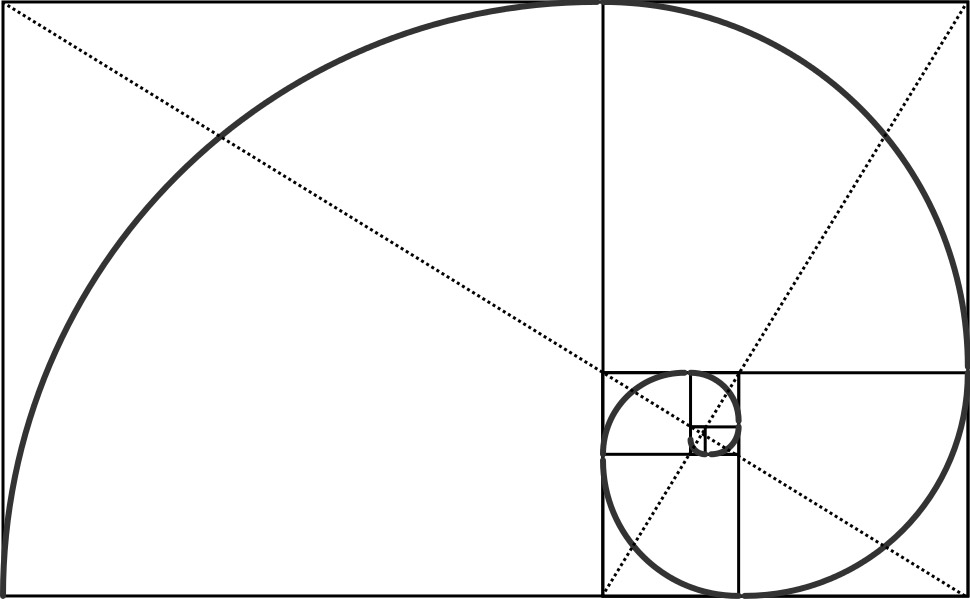
Come vedete dalla figura, è possibile suddividerlo in tanti rettangoli di dimensioni sempre minori:
– basta sottrarre a ciascun rettangolo un quadrato costruito a partire dal lato minore del rettangolo.
– Unendo poi gli angoli dei quadrati contigui, otteniamo la spirale di Fibonacci.
La spirale di Fibonacci rispecchia quella esistente in natura (basti pensare alla conchiglia nautilus) e forse è proprio per questo che l’occhio umano trova tale rapporto particolarmente piacevole.
Seguendo le linee calcolate a partire dalla sezione aurea, è possibile bilanciare la composizione ottenendo un’immagine armoniosa ed equilibrata.
Quando tra le forme regna l’armonia, non c’è più nulla da aggiungere e nulla da togliere, il contenuto riesce a brillare con maggiore evidenza e l’immagine prende vita.
Del resto, le proporzioni del taglio con il quale i fotografi lavorano rispettano già il rapporto aureo: il classico 10×15 altro non è che un rettangolo aureo.
DOPO QUESTO TESTO DI FRANCO FONTANA, FACCIAMO IL PROCEDIMENTO INVERSO, CIOÈ PARTIAMO DA ZERO E COSTRUIAMO UNA SPIRALE AUREA:
Fonte: YouTube – Prof. Lorenzo Bocca
http://boccalorenzo.blogspot.com
Ricapitolando:
1) Il rettangolo aureo deriva da un quadrato. Partiamo da questo quadrato per costruire il primo rettangolo aureo.
2) Man mano che si formano i rettangoli, andiamo a cercare i quadrati che li hanno generati, ribaltando un lato minore di ognuno sul rispettivo lato maggiore.
3) Abbiamo detto che, dato un segmento suddiviso in due parti, la parte maggiore deve stare alla minore come l’intera sta alla maggiore. Il valore di questo rapporto “ideale” tra le due misure è una costante: 1.6180 (arrotondato).

AB : BE = 1.6180
Nel prossimo articolo entreremo più nel dettaglio ma anche noi non ci perderemo in calcoli e formule matematiche.
PER CONCLUDERE, VOGLIAMO MOSTRARVI ALCUNE FOTO IN CUI POSSIAMO APPREZZARE LA BELLEZZA DELLA SEZIONE AUREA:




Leggi QUi l’estratto del libro in cui
l’Autore parla di sezione aurea
***